Code to Read 26 Bits From Keypad
Given the mobile numeric keypad. You tin can merely press buttons that are upward, left, right or down to the current push. You are not allowed to printing bottom row corner buttons (i.due east. * and # ).
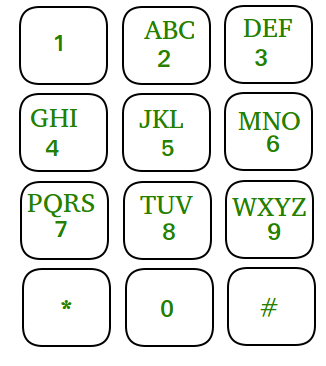
Given a number N, find out the number of possible numbers of given length.
Examples:
For Northward=ane, number of possible numbers would be 10 (0, ane, 2, 3, …., nine)
For N=two, number of possible numbers would be 36
Possible numbers: 00,08 11,12,14 22,21,23,25 and and so on.
If we start with 0, valid numbers volition be 00, 08 (count: 2)
If nosotros start with 1, valid numbers will be 11, 12, 14 (count: three)
If we outset with 2, valid numbers will exist 22, 21, 23,25 (count: iv)
If we starting time with 3, valid numbers volition be 33, 32, 36 (count: 3)
If we kickoff with 4, valid numbers volition be 44,41,45,47 (count: 4)
If we start with 5, valid numbers will be 55,54,52,56,58 (count: 5)
………………………………
………………………………
We need to print the count of possible numbers.
Recommended: Please solve it on " PRACTICE " first, before moving on to the solution.
N = 1 is niggling case, number of possible numbers would be 10 (0, 1, ii, 3, …., 9)
For N > one, we need to start from some button, then move to any of the four direction (upwardly, left, right or down) which takes to a valid button (should not get to *, #). Proceed doing this until N length number is obtained (depth start traversal).
Recursive Solution:
Mobile Keypad is a rectangular filigree of 4X3 (4 rows and 3 columns)
Lets say Count(i, j, N) represents the count of N length numbers starting from position (i, j)
If N = 1 Count(i, j, N) = 10 Else Count(i, j, N) = Sum of all Count(r, c, Northward-1) where (r, c) is new position afterward valid motility of length 1 from current position (i, j)
Following is the implementation of above recursive formula.
C++
#include <stdio.h>
int row[] = {0, 0, -1, 0, 1};
int col[] = {0, -1, 0, 1, 0};
int getCountUtil( char keypad[][3], int i, int j, int due north)
{
if (keypad == NULL || n <= 0)
return 0;
if (north == i)
return ane;
int grand=0, movement=0, ro=0, co=0, totalCount = 0;
for (move=0; move<5; motion++)
{
ro = i + row[motility];
co = j + col[movement];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, north-1);
}
}
render totalCount;
}
int getCount( char keypad[][iii], int northward)
{
if (keypad == Naught || northward <= 0)
render 0;
if (north == 1)
return 10;
int i=0, j=0, totalCount = 0;
for (i=0; i<4; i++)
{
for (j=0; j<three; j++)
{
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
int main( int argc, char *argv[])
{
char keypad[4][3] = {{ '1' , 'ii' , '3' },
{ '4' , '5' , '6' },
{ '7' , 'viii' , '9' },
{ '*' , '0' , '#' }};
printf ( "Count for numbers of length %d: %dn" , 1, getCount(keypad, 1));
printf ( "Count for numbers of length %d: %dn" , 2, getCount(keypad, 2));
printf ( "Count for numbers of length %d: %dn" , 3, getCount(keypad, iii));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , five, getCount(keypad, 5));
return 0;
}
Coffee
class GfG
{
static int row[] = { 0 , 0 , - 1 , 0 , i };
static int col[] = { 0 , - 1 , 0 , 1 , 0 };
static int getCountUtil( char keypad[][],
int i, int j, int n)
{
if (keypad == null || n <= 0 )
render 0 ;
if (n == 1 )
render ane ;
int k = 0 , motility = 0 , ro = 0 , co = 0 , totalCount = 0 ;
for (move= 0 ; move< 5 ; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= iii && co >= 0 && co <= ii &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, n - 1 );
}
}
return totalCount;
}
static int getCount( char keypad[][], int n)
{
if (keypad == zilch || northward <= 0 )
render 0 ;
if (due north == ane )
render x ;
int i = 0 , j = 0 , totalCount = 0 ;
for (i = 0 ; i < iv ; i++)
{
for (j= 0 ; j< three ; j++)
{
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
public static void main(String[] args)
{
char keypad[][] = {{ '1' , '2' , 'three' },
{ 'four' , 'v' , 'six' },
{ '7' , 'viii' , 'ix' },
{ '*' , '0' , '#' }};
Organisation.out.printf( "Count for numbers of" +
" length %d: %d" , i , getCount(keypad, one ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 2 , getCount(keypad, ii ));
Arrangement.out.printf( "\nCount for numbers of" +
"length %d: %d" , 3 , getCount(keypad, 3 ));
Organization.out.printf( "\nCount for numbers of" +
"length %d: %d" , four , getCount(keypad, four ));
System.out.printf( "\nCount for numbers of" +
"length %d: %d" , 5 , getCount(keypad, 5 ));
}
}
Python3
row = [ 0 , 0 , - 1 , 0 , 1 ]
col = [ 0 , - 1 , 0 , 1 , 0 ]
def getCountUtil(keypad, i, j, n):
if (keypad = = None or n < = 0 ):
return 0
if (n = = 1 ):
return 1
chiliad = 0
motion = 0
ro = 0
co = 0
totalCount = 0
for move in range ( v ):
ro = i + row[move]
co = j + col[motion]
if (ro > = 0 and ro < = 3 and co > = 0 and co < = two and
keypad[ro][co] ! = '*' and keypad[ro][co] ! = '#' ):
totalCount + = getCountUtil(keypad, ro, co, n - 1 )
return totalCount
def getCount(keypad, northward):
if (keypad = = None or n < = 0 ):
render 0
if (n = = 1 ):
return 10
i = 0
j = 0
totalCount = 0
for i in range ( 4 ):
for j in range ( 3 ):
if (keypad[i][j] ! = '*' and keypad[i][j] ! = '#' ):
totalCount + = getCountUtil(keypad, i, j, n)
return totalCount
keypad = [[ 'ane' , '2' , 'three' ],
[ '4' , '5' , '6' ],
[ '7' , 'eight' , 'ix' ],
[ '*' , '0' , '#' ]]
print ( "Count for numbers of length i:" , getCount(keypad, i ))
print ( "Count for numbers of length 2:" , getCount(keypad, 2 ))
impress ( "Count for numbers of length 3:" , getCount(keypad, 3 ))
print ( "Count for numbers of length iv:" , getCount(keypad, 4 ))
print ( "Count for numbers of length 5:" , getCount(keypad, five ))
C#
using Organization;
class GfG
{
static int []row = {0, 0, -i, 0, ane};
static int []col = {0, -1, 0, 1, 0};
static int getCountUtil( char [,]keypad,
int i, int j, int north)
{
if (keypad == null || n <= 0)
return 0;
if (due north == one)
render 1;
int 1000 = 0, move = 0, ro = 0, co = 0, totalCount = 0;
for (move=0; motion<v; move++)
{
ro = i + row[move];
co = j + col[movement];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro,co] != '*' && keypad[ro,co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, n - 1);
}
}
render totalCount;
}
static int getCount( char [,]keypad, int n)
{
if (keypad == cypher || n <= 0)
return 0;
if (n == 1)
return 10;
int i = 0, j = 0, totalCount = 0;
for (i = 0; i < 4; i++)
{
for (j = 0; j < 3; j++)
{
if (keypad[i, j] != '*' && keypad[i, j] != '#' )
{
totalCount += getCountUtil(keypad, i, j, due north);
}
}
}
render totalCount;
}
public static void Main()
{
char [,]keypad = {{ 'ane' , '2' , '3' },
{ 'iv' , '5' , '6' },
{ '7' , '8' , 'ix' },
{ '*' , '0' , '#' }};
Panel.Write( "Count for numbers of" +
" length {0}: {1}" , 1, getCount(keypad, 1));
Panel.Write( "\nCount for numbers of" +
"length {0}: {1}" , two, getCount(keypad, 2));
Panel.Write( "\nCount for numbers of" +
"length {0}: {1}" , 3, getCount(keypad, 3));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 4, getCount(keypad, 4));
Console.Write( "\nCount for numbers of" +
"length {0}: {1}" , 5, getCount(keypad, 5));
}
}
PHP
<?php
function getCountUtil( $keypad ,
$i , $j , $n )
{
static $row = array (0,0,-i,0,one);
static $col = assortment (0,-1,0,ane,0);
if ( $keypad == nada || $n <= 0)
render 0;
if ( $north == 1)
render 1;
$k = 0; $move = 0; $ro = 0; $co = 0; $totalCount = 0;
for ( $move = 0; $move < v; $move ++)
{
$ro = $i + $row [ $motion ];
$co = $j + $col [ $move ];
if ( $ro >= 0 && $ro <= iii && $co >=0 && $co <= two &&
$keypad [ $ro ][ $co ] != '*' && $keypad [ $ro ][ $co ] != '#' )
{
$totalCount += getCountUtil( $keypad , $ro , $co , $n - ane);
}
}
return $totalCount ;
}
function getCount( $keypad , $n )
{
if ( $keypad == null || $n <= 0)
return 0;
if ( $due north == ane)
render 10;
$i = 0; $j = 0; $totalCount = 0;
for ( $i = 0; $i < 4; $i ++)
{
for ( $j = 0; $j < 3; $j ++)
{
if ( $keypad [ $i ][ $j ] != '*' && $keypad [ $i ][ $j ] != '#' )
{
$totalCount += getCountUtil( $keypad , $i , $j , $north );
}
}
}
render $totalCount ;
}
{
$keypad = array ( array ( '1' , 'ii' , '3' ),
array ( '4' , '5' , '6' ),
array ( 'vii' , '8' , 'nine' ),
array ( '*' , '0' , '#' ));
repeat ( "Count for numbers of" . " length" . getCount( $keypad , i));
echo ( "\nCount for numbers of" .
" length " . getCount( $keypad , 2));
repeat ( "\nCount for numbers of" .
" length " .getCount( $keypad , 3));
repeat ( "\nCount for numbers of" .
" length " .getCount( $keypad , iv));
echo ( "\nCount for numbers of" .
" length " .getCount( $keypad , v));
}
Javascript
<script>
permit row=[0, 0, -1, 0, one];
let col=[0, -one, 0, 1, 0];
part getCountUtil(keypad,i,j,north)
{
if (keypad == aught || n <= 0)
{ render 0;}
if (n == i)
return 1;
let yard = 0, motility = 0, ro = 0, co = 0, totalCount = 0;
for (move=0; movement<5; move++)
{
ro = i + row[move];
co = j + col[move];
if (ro >= 0 && ro <= three && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
totalCount += getCountUtil(keypad, ro, co, north - 1);
}
}
render totalCount;
}
function getCount(keypad,north)
{
if (keypad == null || n <= 0)
return 0;
if (n == ane)
render 10;
let i = 0, j = 0, totalCount = 0;
for (i = 0; i < 4; i++)
{
for (j=0; j<3; j++)
{
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
totalCount += getCountUtil(keypad, i, j, n);
}
}
}
return totalCount;
}
let keypad=[[ '1' , '2' , 'iii' ],[ 'four' , '5' , '6' ],[ '7' , '8' , '9' ],[ '*' , '0' , '#' ]];
document.write( "Count for numbers of" +
" length " , 1, ": " , getCount(keypad, ane));
certificate.write( "<br>Count for numbers of" +
"length " , 2, ": " , getCount(keypad, ii));
certificate.write( "<br>Count for numbers of" +
"length " , 3, ": " , getCount(keypad, three));
document.write( "<br>Count for numbers of" +
"length " , 4, ": " , getCount(keypad, 4));
document.write( "<br>Count for numbers of" +
"length " , 5, ": " , getCount(keypad, 5));
</script>
Output:
Count for numbers of length one: 10 Count for numbers of length ii: 36 Count for numbers of length 3: 138 Count for numbers of length 4: 532 Count for numbers of length 5: 2062
Dynamic Programming
There are many repeated traversal on smaller paths (traversal for smaller N) to find all possible longer paths (traversal for bigger Due north). See following two diagrams for example. In this traversal, for N = 4 from two starting positions (buttons '4' and 'viii'), nosotros can run across there are few repeated traversals for N = 2 (eastward.g. iv -> 1, 6 -> three, eight -> 9, viii -> 7 etc).
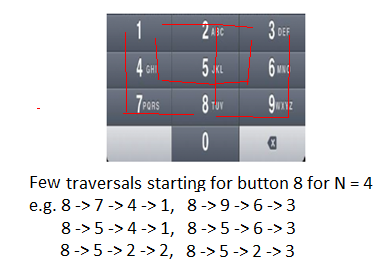
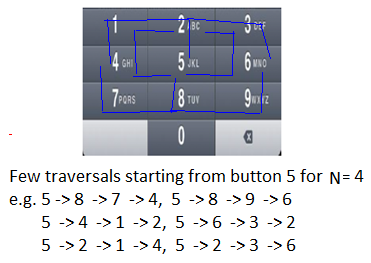
Since the problem has both backdrop: Optimal Substructure and Overlapping Subproblems, it can be efficiently solved using dynamic programming.
Following is the plan for dynamic programming implementation.
C++
#include <stdio.h>
int getCount( char keypad[][3], int n)
{
if (keypad == NULL || north <= 0)
render 0;
if (n == i)
return 10;
int row[] = {0, 0, -one, 0, 1};
int col[] = {0, -1, 0, 1, 0};
int count[10][north+one];
int i=0, j=0, k=0, move=0, ro=0, co=0, num = 0;
int nextNum=0, totalCount = 0;
for (i=0; i<=9; i++)
{
count[i][0] = 0;
count[i][1] = 1;
}
for (k=2; k<=n; 1000++)
{
for (i=0; i<4; i++)
{
for (j=0; j<three; j++)
{
if (keypad[i][j] != '*' && keypad[i][j] != '#' )
{
num = keypad[i][j] - '0' ;
count[num][m] = 0;
for (movement=0; move<v; motion++)
{
ro = i + row[move];
co = j + col[motility];
if (ro >= 0 && ro <= 3 && co >=0 && co <= 2 &&
keypad[ro][co] != '*' && keypad[ro][co] != '#' )
{
nextNum = keypad[ro][co] - '0' ;
count[num][one thousand] += count[nextNum][thou-1];
}
}
}
}
}
}
totalCount = 0;
for (i=0; i<=9; i++)
totalCount += count[i][due north];
return totalCount;
}
int primary( int argc, char *argv[])
{
char keypad[4][3] = {{ 'ane' , '2' , 'iii' },
{ '4' , '5' , 'half dozen' },
{ '7' , '8' , 'ix' },
{ '*' , '0' , '#' }};
printf ( "Count for numbers of length %d: %dn" , 1, getCount(keypad, one));
printf ( "Count for numbers of length %d: %dn" , ii, getCount(keypad, 2));
printf ( "Count for numbers of length %d: %dn" , 3, getCount(keypad, 3));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , 5, getCount(keypad, v));
render 0;
}
Java
class GFG
{
static int getCount( char keypad[][], int n)
{
if (keypad == nil || due north <= 0 )
return 0 ;
if (n == i )
return 10 ;
int row[] = { 0 , 0 , - ane , 0 , 1 };
int col[] = { 0 , - i , 0 , one , 0 };
int [][]count = new int [ 10 ][n + 1 ];
int i = 0 , j = 0 , k = 0 , move = 0 ,
ro = 0 , co = 0 , num = 0 ;
int nextNum = 0 , totalCount = 0 ;
for (i = 0 ; i <= 9 ; i++)
{
count[i][ 0 ] = 0 ;
count[i][ 1 ] = 1 ;
}
for (k = two ; yard <= n; grand++)
{
for (i = 0 ; i < 4 ; i++)
{
for (j = 0 ; j < 3 ; j++)
{
if (keypad[i][j] != '*' &&
keypad[i][j] != '#' )
{
num = keypad[i][j] - '0' ;
count[num][thousand] = 0 ;
for (move = 0 ; move < 5 ; move++)
{
ro = i + row[movement];
co = j + col[move];
if (ro >= 0 && ro <= 3 && co >= 0 &&
co <= ii && keypad[ro][co] != '*' &&
keypad[ro][co] != '#' )
{
nextNum = keypad[ro][co] - '0' ;
count[num][k] += count[nextNum][thou - 1 ];
}
}
}
}
}
}
totalCount = 0 ;
for (i = 0 ; i <= 9 ; i++)
totalCount += count[i][northward];
return totalCount;
}
public static void main(Cord[] args)
{
char keypad[][] = {{ '1' , '2' , '3' },
{ '4' , '5' , '6' },
{ 'seven' , '8' , '9' },
{ '*' , '0' , '#' }};
Organization.out.printf( "Count for numbers of length %d: %d\n" , 1 ,
getCount(keypad, 1 ));
System.out.printf( "Count for numbers of length %d: %d\north" , 2 ,
getCount(keypad, 2 ));
Arrangement.out.printf( "Count for numbers of length %d: %d\n" , iii ,
getCount(keypad, iii ));
System.out.printf( "Count for numbers of length %d: %d\n" , 4 ,
getCount(keypad, 4 ));
Organisation.out.printf( "Count for numbers of length %d: %d\n" , 5 ,
getCount(keypad, v ));
}
}
Python3
def getCount(keypad, n):
if (keypad = = None or n < = 0 ):
return 0
if (n = = 1 ):
return ten
row = [ 0 , 0 , - 1 , 0 , one ]
col = [ 0 , - ane , 0 , 1 , 0 ]
count = [[ 0 ] * (n + 1 )] * 10
i = 0
j = 0
thousand = 0
move = 0
ro = 0
co = 0
num = 0
nextNum = 0
totalCount = 0
for i in range ( ten ):
count[i][ 0 ] = 0
count[i][ 1 ] = 1
for grand in range ( 2 , n + 1 ):
for i in range ( iv ):
for j in range ( 3 ):
if (keypad[i][j] ! = '*' and keypad[i][j] ! = '#' ):
num = ord (keypad[i][j]) - 48
count[num][m] = 0
for move in range ( 5 ):
ro = i + row[move]
co = j + col[move]
if (ro > = 0 and ro < = iii and co > = 0 and co < = 2 and
keypad[ro][co] ! = '*' and keypad[ro][co] ! = '#' ):
nextNum = ord (keypad[ro][co]) - 48
count[num][k] + = count[nextNum][one thousand - 1 ]
totalCount = 0
for i in range ( ten ):
totalCount + = count[i][north]
return totalCount
if __name__ = = "__main__" :
keypad = [[ 'i' , 'ii' , '3' ],
[ '4' , 'five' , 'vi' ],
[ '7' , '8' , '9' ],
[ '*' , '0' , '#' ]]
print ( "Count for numbers of length" , one , ":" , getCount(keypad, i ))
print ( "Count for numbers of length" , 2 , ":" , getCount(keypad, 2 ))
impress ( "Count for numbers of length" , iii , ":" , getCount(keypad, 3 ))
print ( "Count for numbers of length" , iv , ":" , getCount(keypad, iv ))
impress ( "Count for numbers of length" , 5 , ":" , getCount(keypad, 5 ))
C#
using Arrangement;
grade GFG
{
static int getCount( char [,]keypad, int northward)
{
if (keypad == null || northward <= 0)
return 0;
if (due north == i)
return 10;
int []row = {0, 0, -1, 0, ane};
int []col = {0, -1, 0, 1, 0};
int [,]count = new int [10,n + one];
int i = 0, j = 0, k = 0, motility = 0,
ro = 0, co = 0, num = 0;
int nextNum = 0, totalCount = 0;
for (i = 0; i <= ix; i++)
{
count[i, 0] = 0;
count[i, 1] = 1;
}
for (1000 = two; k <= due north; k++)
{
for (i = 0; i < 4; i++)
{
for (j = 0; j < three; j++)
{
if (keypad[i, j] != '*' &&
keypad[i, j] != '#' )
{
num = keypad[i, j] - '0' ;
count[num, k] = 0;
for (move = 0; move < 5; move++)
{
ro = i + row[motion];
co = j + col[motion];
if (ro >= 0 && ro <= 3 && co >= 0 &&
co <= 2 && keypad[ro, co] != '*' &&
keypad[ro, co] != '#' )
{
nextNum = keypad[ro, co] - '0' ;
count[num, 1000] += count[nextNum, grand - ane];
}
}
}
}
}
}
totalCount = 0;
for (i = 0; i <= nine; i++)
totalCount += count[i, northward];
return totalCount;
}
public static void Master(String[] args)
{
char [,]keypad = {{ 'ane' , '2' , 'three' },
{ 'iv' , '5' , 'six' },
{ 'vii' , '8' , '9' },
{ '*' , '0' , '#' }};
Console.Write( "Count for numbers of.Length {0}: {1}\n" , 1,
getCount(keypad, 1));
Panel.Write( "Count for numbers of.Length {0}: {1}\n" , 2,
getCount(keypad, 2));
Panel.Write( "Count for numbers of.Length {0}: {1}\northward" , iii,
getCount(keypad, 3));
Panel.Write( "Count for numbers of.Length {0}: {1}\n" , iv,
getCount(keypad, 4));
Panel.Write( "Count for numbers of.Length {0}: {i}\n" , 5,
getCount(keypad, 5));
}
}
Javascript
<script>
function getCount(keypad, north)
{
if (keypad == aught || due north <= 0)
return 0;
if (northward == one)
return 10;
let row = [ 0, 0, -1, 0, 1 ];
let col = [ 0, -i, 0, 1, 0 ];
allow count = new Array(ten);
for (let i = 0; i < 10; i++)
{
count[i] = new Array(n + 1);
for (let j = 0; j < n + 1; j++)
{
count[i][j] = 0;
}
}
let i = 0, j = 0, one thousand = 0, move = 0,
ro = 0, co = 0, num = 0;
permit nextNum = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
{
count[i][0] = 0;
count[i][i] = one;
}
for (yard = two; k <= n; yard++)
{
for (i = 0; i < 4; i++)
{
for (j = 0; j < 3; j++)
{
if (keypad[i][j] != '*' &&
keypad[i][j] != '#' )
{
num = keypad[i][j].charCodeAt(0) -
'0' .charCodeAt(0);
count[num][grand] = 0;
for (move = 0; motility < 5; move++)
{
ro = i + row[move];
co = j + col[movement];
if (ro >= 0 && ro <= iii && co >= 0 &&
co <= two && keypad[ro][co] != '*' &&
keypad[ro][co] != '#' )
{
nextNum = keypad[ro][co].charCodeAt(0) -
'0' .charCodeAt(0);
count[num][k] += count[nextNum][one thousand - 1];
}
}
}
}
}
}
totalCount = 0;
for (i = 0; i <= 9; i++)
totalCount += count[i][northward];
return totalCount;
}
let keypad = [ [ 'one' , 'ii' , '3' ],
[ '4' , '5' , '6' ],
[ '7' , '8' , '9' ],
[ '*' , '0' , '#' ] ];
certificate.write( "Count for numbers of length " +
1 + " : " + getCount(keypad, 1) + "<br>" )
document.write( "Count for numbers of length " +
2 + " : " + getCount(keypad, 2) + "<br>" )
document.write( "Count for numbers of length " +
3 + " : " + getCount(keypad, 3) + "<br>" )
document.write( "Count for numbers of length " +
4 + " : " + getCount(keypad, 4) + "<br>" )
certificate.write( "Count for numbers of length " +
v + " : " + getCount(keypad, 5) + "<br>" )
</script>
Output:
Count for numbers of length 1: 10 Count for numbers of length 2: 36 Count for numbers of length three: 138 Count for numbers of length 4: 532 Count for numbers of length 5: 2062
A Space Optimized Solution:
The to a higher place dynamic programming approach too runs in O(n) time and requires O(north) auxiliary space, as just one for loop runs n times, other for loops runs for abiding time. We tin see that nth iteration needs data from (n-1)thursday iteration just, and so nosotros demand non keep the information from older iterations. Nosotros can have a space efficient dynamic programming approach with just two arrays of size x. Cheers to Nik for suggesting this solution.
C++
#include <$.25/stdc++.h>
using namespace std;
int getCount( char keypad[][3], int n)
{
if (keypad == Cipher || due north <= 0)
return 0;
if (n == 1)
return 10;
int odd[10], even[10];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1;
for (j = ii; j <= n; j++)
{
useOdd = i - useOdd;
if (useOdd == ane)
{
fifty-fifty[0] = odd[0] + odd[eight];
even[1] = odd[i] + odd[ii] + odd[4];
fifty-fifty[ii] = odd[2] + odd[1] + odd[three] + odd[five];
fifty-fifty[3] = odd[3] + odd[2] + odd[6];
even[four] = odd[iv] + odd[1] + odd[5] + odd[7];
even[5] = odd[5] + odd[ii] + odd[4] + odd[8] + odd[half dozen];
fifty-fifty[six] = odd[6] + odd[3] + odd[5] + odd[nine];
even[vii] = odd[7] + odd[4] + odd[8];
even[eight] = odd[8] + odd[0] + odd[5] + odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[eight];
}
else
{
odd[0] = fifty-fifty[0] + fifty-fifty[eight];
odd[1] = even[1] + even[2] + fifty-fifty[4];
odd[2] = fifty-fifty[ii] + even[1] + even[3] + even[5];
odd[3] = even[3] + fifty-fifty[2] + even[vi];
odd[iv] = even[four] + fifty-fifty[1] + fifty-fifty[5] + even[vii];
odd[5] = even[5] + even[2] + fifty-fifty[4] + even[8] + even[vi];
odd[6] = even[6] + even[iii] + fifty-fifty[5] + even[9];
odd[7] = even[7] + fifty-fifty[4] + even[8];
odd[8] = even[viii] + even[0] + fifty-fifty[5] + fifty-fifty[7] + even[9];
odd[9] = even[nine] + fifty-fifty[six] + even[8];
}
}
totalCount = 0;
if (useOdd == 1)
{
for (i = 0; i <= 9; i++)
totalCount += fifty-fifty[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
int principal()
{
char keypad[4][iii] = {{ '1' , '2' , '3' },
{ '4' , '5' , '6' },
{ 'vii' , '8' , '9' },
{ '*' , '0' , '#' }};
cout << "Count for numbers of length 1: " << getCount(keypad, ane) << endl;
cout << "Count for numbers of length 2: " << getCount(keypad, 2) << endl;
cout << "Count for numbers of length 3: " << getCount(keypad, iii) << endl;
cout << "Count for numbers of length four: " << getCount(keypad, 4) << endl;
cout << "Count for numbers of length 5: " << getCount(keypad, five) << endl;
return 0;
}
C
#include <stdio.h>
int getCount( char keypad[][three], int north)
{
if (keypad == Nix || n <= 0)
render 0;
if (n == one)
return 10;
int odd[10], fifty-fifty[ten];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i=0; i<=9; i++)
odd[i] = 1;
for (j=2; j<=n; j++)
{
useOdd = 1 - useOdd;
if (useOdd == 1)
{
even[0] = odd[0] + odd[eight];
even[ane] = odd[1] + odd[2] + odd[4];
even[2] = odd[ii] + odd[1] + odd[three] + odd[5];
even[3] = odd[three] + odd[2] + odd[six];
even[4] = odd[4] + odd[1] + odd[v] + odd[7];
even[five] = odd[v] + odd[2] + odd[iv] + odd[8] + odd[vi];
even[six] = odd[6] + odd[3] + odd[v] + odd[ix];
fifty-fifty[7] = odd[7] + odd[4] + odd[8];
even[8] = odd[8] + odd[0] + odd[v] + odd[7] + odd[9];
even[9] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + even[eight];
odd[i] = even[i] + even[2] + even[iv];
odd[ii] = even[ii] + fifty-fifty[one] + even[3] + fifty-fifty[5];
odd[3] = fifty-fifty[iii] + even[two] + even[six];
odd[4] = even[4] + even[1] + fifty-fifty[5] + even[7];
odd[5] = even[5] + even[ii] + even[4] + fifty-fifty[8] + even[6];
odd[6] = even[6] + fifty-fifty[iii] + fifty-fifty[5] + even[ix];
odd[7] = fifty-fifty[vii] + even[4] + even[eight];
odd[8] = even[8] + even[0] + fifty-fifty[5] + even[7] + even[9];
odd[9] = even[ix] + even[half-dozen] + even[eight];
}
}
totalCount = 0;
if (useOdd == one)
{
for (i=0; i<=nine; i++)
totalCount += even[i];
}
else
{
for (i=0; i<=nine; i++)
totalCount += odd[i];
}
render totalCount;
}
int main()
{
char keypad[4][3] = {{ '1' , '2' , 'iii' },
{ 'iv' , '5' , '6' },
{ 'vii' , 'eight' , '9' },
{ '*' , '0' , '#' }
};
printf ( "Count for numbers of length %d: %dn" , i, getCount(keypad, i));
printf ( "Count for numbers of length %d: %dn" , 2, getCount(keypad, two));
printf ( "Count for numbers of length %d: %dn" , three, getCount(keypad, 3));
printf ( "Count for numbers of length %d: %dn" , 4, getCount(keypad, 4));
printf ( "Count for numbers of length %d: %dn" , 5, getCount(keypad, v));
return 0;
}
Java
grade GFG
{
static int getCount( char keypad[][], int n)
{
if (keypad == null || n <= 0 )
return 0 ;
if (northward == ane )
return 10 ;
int []odd = new int [ 10 ];
int []even = new int [ 10 ];
int i = 0 , j = 0 , useOdd = 0 , totalCount = 0 ;
for (i = 0 ; i <= 9 ; i++)
odd[i] = 1 ;
for (j = 2 ; j <= n; j++)
{
useOdd = 1 - useOdd;
if (useOdd == 1 )
{
fifty-fifty[ 0 ] = odd[ 0 ] + odd[ 8 ];
even[ one ] = odd[ 1 ] + odd[ 2 ] + odd[ 4 ];
even[ 2 ] = odd[ two ] + odd[ 1 ] +
odd[ iii ] + odd[ 5 ];
fifty-fifty[ 3 ] = odd[ 3 ] + odd[ 2 ] + odd[ 6 ];
even[ iv ] = odd[ 4 ] + odd[ ane ] +
odd[ v ] + odd[ 7 ];
fifty-fifty[ v ] = odd[ five ] + odd[ ii ] + odd[ 4 ] +
odd[ 8 ] + odd[ 6 ];
even[ six ] = odd[ half-dozen ] + odd[ three ] +
odd[ five ] + odd[ 9 ];
even[ 7 ] = odd[ seven ] + odd[ 4 ] + odd[ 8 ];
fifty-fifty[ 8 ] = odd[ 8 ] + odd[ 0 ] + odd[ 5 ] +
odd[ 7 ] + odd[ nine ];
even[ 9 ] = odd[ 9 ] + odd[ 6 ] + odd[ 8 ];
}
else
{
odd[ 0 ] = even[ 0 ] + even[ eight ];
odd[ i ] = even[ 1 ] + fifty-fifty[ 2 ] + even[ iv ];
odd[ 2 ] = even[ 2 ] + even[ one ] +
fifty-fifty[ 3 ] + even[ five ];
odd[ 3 ] = fifty-fifty[ iii ] + fifty-fifty[ 2 ] + even[ 6 ];
odd[ 4 ] = even[ 4 ] + even[ i ] +
even[ five ] + even[ 7 ];
odd[ v ] = even[ 5 ] + fifty-fifty[ 2 ] + fifty-fifty[ 4 ] +
even[ 8 ] + even[ 6 ];
odd[ 6 ] = even[ half dozen ] + even[ 3 ] +
even[ 5 ] + fifty-fifty[ 9 ];
odd[ vii ] = fifty-fifty[ 7 ] + even[ 4 ] + even[ 8 ];
odd[ 8 ] = fifty-fifty[ 8 ] + even[ 0 ] + even[ five ] +
even[ vii ] + even[ 9 ];
odd[ 9 ] = fifty-fifty[ 9 ] + even[ 6 ] + even[ 8 ];
}
}
totalCount = 0 ;
if (useOdd == 1 )
{
for (i = 0 ; i <= ix ; i++)
totalCount += even[i];
}
else
{
for (i = 0 ; i <= 9 ; i++)
totalCount += odd[i];
}
return totalCount;
}
public static void main(String[] args)
{
char keypad[][] = {{ '1' , '2' , '3' },
{ '4' , '5' , '6' },
{ '7' , '8' , '9' },
{ '*' , '0' , '#' }};
Arrangement.out.printf( "Count for numbers of length %d: %d\n" , 1 ,
getCount(keypad, 1 ));
Organisation.out.printf( "Count for numbers of length %d: %d\northward" , 2 ,
getCount(keypad, ii ));
System.out.printf( "Count for numbers of length %d: %d\northward" , iii ,
getCount(keypad, 3 ));
Organization.out.printf( "Count for numbers of length %d: %d\n" , 4 ,
getCount(keypad, four ));
Arrangement.out.printf( "Count for numbers of length %d: %d\n" , v ,
getCount(keypad, 5 ));
}
}
Python3
def getCount(keypad, n):
if ( not keypad or n < = 0 ):
render 0
if (n = = 1 ):
return 10
odd = [ 0 ] * ten
even = [ 0 ] * 10
i = 0
j = 0
useOdd = 0
totalCount = 0
for i in range ( 10 ):
odd[i] = one
for j in range ( 2 ,n + one ):
useOdd = 1 - useOdd
if (useOdd = = 1 ):
fifty-fifty[ 0 ] = odd[ 0 ] + odd[ eight ]
even[ 1 ] = odd[ ane ] + odd[ two ] + odd[ four ]
even[ 2 ] = odd[ 2 ] + odd[ one ] + odd[ three ] + odd[ 5 ]
fifty-fifty[ iii ] = odd[ iii ] + odd[ two ] + odd[ 6 ]
even[ 4 ] = odd[ iv ] + odd[ one ] + odd[ 5 ] + odd[ 7 ]
even[ 5 ] = odd[ v ] + odd[ 2 ] + odd[ 4 ] + odd[ eight ] + odd[ half-dozen ]
fifty-fifty[ 6 ] = odd[ 6 ] + odd[ 3 ] + odd[ 5 ] + odd[ ix ]
even[ 7 ] = odd[ seven ] + odd[ 4 ] + odd[ viii ]
even[ 8 ] = odd[ 8 ] + odd[ 0 ] + odd[ 5 ] + odd[ 7 ] + odd[ 9 ]
fifty-fifty[ 9 ] = odd[ 9 ] + odd[ half-dozen ] + odd[ viii ]
else :
odd[ 0 ] = even[ 0 ] + even[ 8 ]
odd[ 1 ] = fifty-fifty[ 1 ] + even[ 2 ] + even[ four ]
odd[ 2 ] = even[ two ] + even[ 1 ] + fifty-fifty[ iii ] + even[ 5 ]
odd[ 3 ] = even[ iii ] + even[ 2 ] + even[ six ]
odd[ four ] = even[ 4 ] + fifty-fifty[ 1 ] + even[ v ] + fifty-fifty[ vii ]
odd[ five ] = even[ five ] + fifty-fifty[ two ] + fifty-fifty[ four ] + even[ 8 ] + even[ 6 ]
odd[ half-dozen ] = even[ 6 ] + even[ 3 ] + even[ 5 ] + even[ 9 ]
odd[ 7 ] = even[ seven ] + even[ 4 ] + even[ 8 ]
odd[ 8 ] = even[ eight ] + fifty-fifty[ 0 ] + even[ 5 ] + even[ vii ] + even[ 9 ]
odd[ 9 ] = even[ 9 ] + even[ 6 ] + fifty-fifty[ 8 ]
totalCount = 0
if (useOdd = = 1 ):
for i in range ( 10 ):
totalCount + = even[i]
else :
for i in range ( x ):
totalCount + = odd[i]
return totalCount
if __name__ = = "__main__" :
keypad = [[ '1' , '2' , '3' ],
[ '4' , '5' , 'six' ],
[ '7' , '8' , '9' ],
[ '*' , '0' , '#' ]]
print ( "Count for numbers of length " , ane , ": " , getCount(keypad, 1 ))
impress ( "Count for numbers of length " , 2 , ": " , getCount(keypad, ii ))
print ( "Count for numbers of length " , 3 , ": " , getCount(keypad, iii ))
print ( "Count for numbers of length " , iv , ": " , getCount(keypad, iv ))
print ( "Count for numbers of length " , v , ": " , getCount(keypad, 5 ))
C#
using System;
class GFG
{
static int getCount( char [,]keypad, int n)
{
if (keypad == cypher || n <= 0)
return 0;
if (n == ane)
return 10;
int []odd = new int [10];
int []fifty-fifty = new int [x];
int i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= 9; i++)
odd[i] = 1;
for (j = 2; j <= n; j++)
{
useOdd = i - useOdd;
if (useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[ii] + odd[4];
fifty-fifty[2] = odd[2] + odd[1] +
odd[three] + odd[5];
even[three] = odd[iii] + odd[2] + odd[6];
even[4] = odd[four] + odd[one] +
odd[5] + odd[vii];
even[5] = odd[5] + odd[ii] + odd[4] +
odd[8] + odd[half-dozen];
even[vi] = odd[6] + odd[iii] +
odd[v] + odd[9];
fifty-fifty[seven] = odd[7] + odd[4] + odd[eight];
fifty-fifty[8] = odd[8] + odd[0] + odd[5] +
odd[7] + odd[9];
even[9] = odd[nine] + odd[six] + odd[8];
}
else
{
odd[0] = even[0] + even[viii];
odd[1] = even[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + fifty-fifty[five];
odd[3] = even[3] + fifty-fifty[2] + even[6];
odd[4] = even[4] + even[1] +
even[5] + even[vii];
odd[5] = even[5] + even[2] + fifty-fifty[four] +
even[8] + fifty-fifty[6];
odd[half dozen] = fifty-fifty[6] + even[3] +
even[5] + even[nine];
odd[vii] = even[7] + fifty-fifty[4] + fifty-fifty[eight];
odd[8] = fifty-fifty[viii] + even[0] + even[5] +
even[7] + fifty-fifty[9];
odd[9] = even[9] + even[6] + even[8];
}
}
totalCount = 0;
if (useOdd == 1)
{
for (i = 0; i <= nine; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= 9; i++)
totalCount += odd[i];
}
return totalCount;
}
public static void Main(String[] args)
{
char [,]keypad = {{ '1' , '2' , 'three' },
{ '4' , '5' , '6' },
{ 'seven' , '8' , 'nine' },
{ '*' , '0' , '#' }};
Console.Write( "Count for numbers of length {0}: {one}\n" , 1,
getCount(keypad, one));
Console.Write( "Count for numbers of length {0}: {1}\n" , two,
getCount(keypad, ii));
Console.Write( "Count for numbers of length {0}: {1}\northward" , 3,
getCount(keypad, 3));
Console.Write( "Count for numbers of length {0}: {1}\due north" , 4,
getCount(keypad, 4));
Panel.Write( "Count for numbers of length {0}: {one}\n" , five,
getCount(keypad, 5));
}
}
Javascript
<script>
part getCount(keypad , northward)
{
if (keypad == null || n <= 0)
return 0;
if (n == 1)
return x;
var odd = Assortment.from({length: 10}, (_, i) => 0);
var even = Array.from({length: 10}, (_, i) => 0);
var i = 0, j = 0, useOdd = 0, totalCount = 0;
for (i = 0; i <= ix; i++)
odd[i] = 1;
for (j = 2; j <= n; j++)
{
useOdd = 1 - useOdd;
if (useOdd == 1)
{
even[0] = odd[0] + odd[8];
even[1] = odd[1] + odd[2] + odd[4];
even[2] = odd[2] + odd[1] +
odd[3] + odd[v];
fifty-fifty[iii] = odd[3] + odd[2] + odd[vi];
even[4] = odd[4] + odd[one] +
odd[v] + odd[vii];
even[5] = odd[5] + odd[2] + odd[4] +
odd[8] + odd[six];
even[6] = odd[6] + odd[3] +
odd[5] + odd[9];
fifty-fifty[7] = odd[seven] + odd[4] + odd[8];
even[8] = odd[viii] + odd[0] + odd[5] +
odd[7] + odd[9];
even[nine] = odd[9] + odd[6] + odd[8];
}
else
{
odd[0] = even[0] + fifty-fifty[viii];
odd[i] = fifty-fifty[1] + even[2] + even[4];
odd[2] = even[2] + even[1] +
even[3] + even[5];
odd[3] = even[3] + even[2] + fifty-fifty[vi];
odd[4] = even[4] + even[one] +
fifty-fifty[5] + even[7];
odd[v] = fifty-fifty[v] + even[ii] + even[4] +
even[8] + even[half-dozen];
odd[half-dozen] = even[6] + even[3] +
even[5] + even[ix];
odd[7] = even[vii] + even[4] + even[8];
odd[8] = even[8] + even[0] + even[5] +
even[7] + even[9];
odd[9] = even[ix] + even[6] + even[8];
}
}
totalCount = 0;
if (useOdd == i)
{
for (i = 0; i <= 9; i++)
totalCount += even[i];
}
else
{
for (i = 0; i <= nine; i++)
totalCount += odd[i];
}
return totalCount;
}
var keypad = [[ '1' , '2' , '3' ],
[ 'four' , '5' , 'vi' ],
[ 'seven' , '8' , 'nine' ],
[ '*' , '0' , '#' ]];
certificate.write( "Count for numbers of length " + 1+ ": " +
getCount(keypad, i));
document.write( "<br>Count for numbers of length " + two+ ": " +
getCount(keypad, 2));
document.write( "<br>Count for numbers of length " + 3+ ": " +
getCount(keypad, iii));
document.write( "<br>Count for numbers of length " + 4+ ": " +
getCount(keypad, four));
certificate.write( "<br>Count for numbers of length " + 5+ ": " +
getCount(keypad, 5));
</script>
Output:
Count for numbers of length i: x Count for numbers of length 2: 36 Count for numbers of length 3: 138 Count for numbers of length 4: 532 Count for numbers of length 5: 2062
This article is contributed past Anurag Singh. Delight write comments if you observe annihilation incorrect, or you want to share more information nigh the topic discussed to a higher place.
Source: https://www.geeksforgeeks.org/mobile-numeric-keypad-problem/
0 Response to "Code to Read 26 Bits From Keypad"
Post a Comment